二次筛法

发表于
主要针对 SPQS 和 MQPS 的学习笔记，其中开头部分对费马分解法有简要的概括。对于算因子基的选取、MPQS的多项式参数选取的原理还没有弄懂。

简介

二次筛法(Quadratic Seive)是由Pomerance于1981年提出的，直到1993年是世界上渐进最快的通用大整数因子分解方法，第一的位置后来被数域筛所取代，不过对于120位以下的整数，二次筛还是要比数域筛快一些。了解二次筛法前，需要先了解下费马分解法，因为二次筛法是来源于费马分解法的。

费马分解法

以分解大数 为例，我们试图先找一对具有以下关系的平方数： 如果能找到以上关系的，那我们可以继续变形得到： 这说明 ，那么我们很有可能找到 （或 ）。 此时 所以，在费马分解法的指导下，我们只需要找到 即可。然而，如果盲目去尝试，这样的 也是很不容易找到的。二次筛法的发明，就是帮助我们有步骤地、有效地找到满足以上条件的 关系。

SPQS

多项式构造

在二次筛法中，我们先构造一个二次函数： 由此，我们可得：

一般情况下 ，此时

因子基

由上面的式子可得，我们可以看出 已经是一个平方数了，因此下一步我们的目的就是想方设法构造一个 是一个完全平方数（在模的意义下）。显然，直接去找这样的 是效率非常低的。我们可以先找一系列能够被某个质数集合完全分解的 ，再寻找一种组合使得他们的乘积是一个平方数。而这个质数集就被称为因子基。一般地，我们记这个因子基为：

其中能够被因子基中的质数完全分解的数，我们称为其是 光滑的。

另外在选取 时，我们仅选取 满足 ，这一点我们将在 3.3 中进行介绍

线性组合

如上文所述，我们并不直接获取 ，而是先确定因子基，再得到一系列 光滑的 。当收集到足够的 后，就可以将满足最终要求的 构造出来。

假设在 的情况下，即搜索区间的长度 ，有一系列光滑的

我们将其记作 ，则 显然右边的式子已经是完全平方数了，而左边由于 是关于 光滑的，因此我们应当选择合适 ，确保乘积结果的 所有质因子 的幂均为偶数，而这本质上就是一个解线性方程组的过程。

下面证明对于任意奇素数 ，仅 时，该奇素数对求解上述方程组的解是有贡献的。

对任意 （注意这里 ，更一般地有 ）有 若存在 ，使得 ，那么有 也就是 是模 下的一个二次剩余，所以我们仅需考虑奇素数 ，使得 。（不然 对应列均为0）

example

下面我们举一例进行说明，这里取

首先选择因子基 (其他素数被删去，因为对于这些素数来说，) 

1
2
3
4
5
N = 15347
factor_base = [2]
for i in range(3, 100):
    if isPrime(i) and kronecker(N, i) == 1:
        factor_base.append(i)

选取 ​。 

1
2
3
4
sqtN = floor(N^0.5)
Q = lambda x: (x+sqtN)^2 - N
upper = int((2*N)^0.5) - sqtN
T = [Q(i) for i in range(1, upper)]

利用筛法进行筛选：分别用集合中的元素出去因子基中的素数 

1
2
3
4
5
6
7
8
9
10
11
12
TT = [[i] for i in T]
for pri in factor_base:
    for j in range(len(T)):
        if TT[j][0] % pri == 0:
            TT[j].append([pri, 0])
        while TT[j][0] % pri == 0:
            TT[j][0] //= pri
            TT[j][-1][1] += 1
            
for i in range(len(T)):
    if TT[i][0] == 1:
        print(T[i], TT[i])

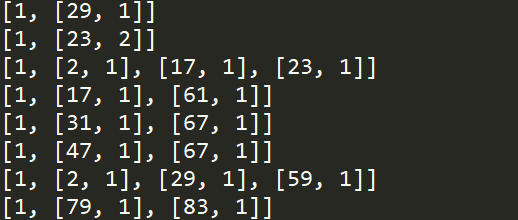
最终得到结果如下表：

的分解对应因子基 上的指数向量
1 29
3 529
4 782
5 1037
9 2077
13 3149
14 3422
25 6557

由上面的表格我们不难看出很明显 直接满足条件。那么我们就有：

此时 至此我们成功分解了 。

算法简述

  • 选取因子基 ，其中 满足： 是素数，
  • 计算出一系列的
  • 通过筛法找到对于因子基 是光滑的所有
  • 根据 构造指数矩阵。
  • 尝试找到矩阵 ，满足 。
  • 如果找不到矩阵 ，回到第3步并扩大 的取值范围

MPQS

对于单个多项式的二次筛法（SPQS）而言，这种方法的主要困难在于，必须得到于因子基中素数差不多多的 为完全平方数，为了得到足够的完全平方数， 的取值范围 中 必须非常大(当然其仍远小于 )，并且完全平方数的大小随 线性增长。

相对而言，MPQS是对上述只用一个二次多项式的SPQS方法的一个改进，可以使用更多的二次多项式并行搜索（相当于非朴素并行化的改进），从而减小因子基 的大小和搜索区间的长度。

多项式构造

我们选择 形式的多项式（），配方得 。

若我们选择，使得 ，此时有： 用 做一个线性代换，就有： 由上述表达式，我们可以求得 的极小点为 ，此时 的值取得最小值为 。

假设我们选择 ，此时 的最大值和最小值的差（极差）为： 而对于算法的计算复杂度来说，我们希望这个极差越小越好，又因为 ，故我们令 。

同时我们期望 ，此时有 ，即 。因此可以选取 为一个接近 的素数

  1. 关于为什么 ？

当且仅当 时我们有，

此时对于任意 ，才有 ​，至此我们才能对因子基运用二次剩余进行筛选，不然同余方程右侧为 ，不容易进行筛选

  1. 为什么选取 为素数？

选取素数可以保证 较容易解出

  1. 为什么 要接近

选取 接近 可以保证极差较小，即 点值较小，减少基础运算的时间复杂度

选择系数的过程可以如下进行：

  • 选择区间长度 。
  • 选择接近于的素数 。
  • 求解 （求解这种离散对数问题用shanks、pollard's rho、Pohlig-Hellman算法）。
  • 令

在 3.1 中，我们有如下等式： 而在本节中，我们可以得到以下式子： 二者在形态上已经完全一致，故可以重复上面的因子基构造的过程。

0%