Pollard Rho

发表于
关于Pollard Rho 算法的笔记

简介

Pollard rho算法是一种用于整数因子分解的有效算法，由Pollard于1975年提出。该算法的核心思想是基于随机化方法，通过在一个循环中生成一个伪随机序列，以期找到大整数的非平凡因子。Pollard rho算法在理论上具有较高的效率，尤其适用于分解具有较小因子的大整数。本文将详细介绍Pollard rho算法的基本原理、步骤及其在整数因子分解领域的应用。

生日悖论

生日悖论其实不是一个逻辑悖论，只是与很多人的第一感觉不符。它可以表述为： 一个房间里有23个人，则他们中有两人生日相同的概率超过一半 （不考虑闰年）。其实这在数学上很好证明，即 。

生日悖论启示我们，如果我们不断在某个范围内生成随机整数，很快便会生成到重复的数，期望大约在根号级别。精确地说，对于一个内整数的理想随机数生成器，生成序列中第一个重复数字前期望有个数

算法思想

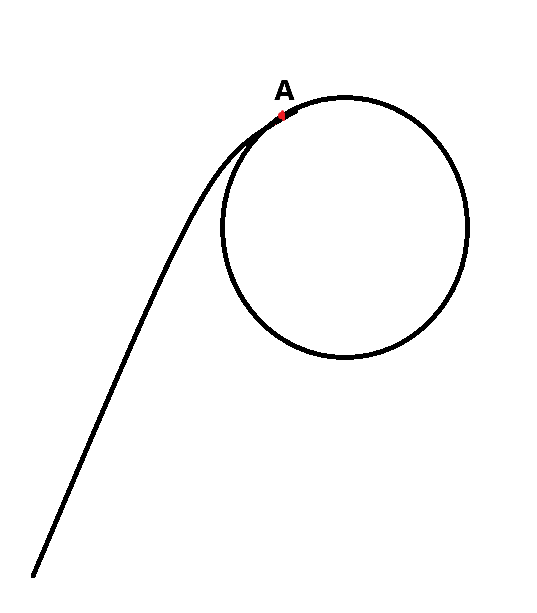
考虑一个序列 其中 ， 为带分解的数， 表示 模 的余数。这里也可以使用其他多项式，一起不同的初始值 ()。我们依次生成三元组 ，这里 对于每个三元组 ，均可以由其前一项 经过 3 次 式操作(得到)和 1 次模乘法操作 (得到 ) 得到。因此，每次迭代涉及的工作基本上是4次模乘法。

当 是某个数 的倍数时 (例如 )， 我们计算最大公因数(这一步事实上为批处理的优化，减少进行求最大公因数的操作，这一点我们将在第三部分优化中详细讲述)； 此时如果有 ，那么我们可以得到 的部分分解为 。这里 可能仍然是合数，如果是这样，则我们继续对上述操作。值得一提的是，下面我们有两种做法，一种是使用一个新的初始点，重新计算新的序列；一种是在上述 的基础上继续进行计算（对于 我们不需要再进行计算，因为我们已经检验对于上述的 有 ，那么 是显然的）

理论

我们考虑 ，由于 ，根据鸽巢原理可以知道上述数列 是有周期的。也就是说，有整数 和 ，使得 都是不同的，但 （这就是为什么该方法的名称是 方法；这里的 必须从底部开始绘制，其大致如下图所示）。

同时我们定义 为 ​ 的最小正整数，即 一个比较直观的理解是，当 第一次到上图点A时，此时 且 同样位于圆上一点，并且此后两者均只在圆上移动。由于 的步长大于 ，后续过程可以看作圆上的一个追及问题。两者的初始距离为 ，故 这种形式与上述结论是一致的。

也就是我们可以在 次计算后可以找到 ，此时我们有很大概率有

假设 在模 上是一个相对随机的映射，那么根据生日悖论， 的期望如下 （事实上这里还有更精确的估计，具体可以参考文献 《A MONTE CARLO METHOD FOR FACTORIZATION》）

至此可以得到，对于合数 ，我们可以在期望时间复杂度 下得到其因子

参考代码

下面为笔者自行实现的 rho 方法参考代码，其中素性检测使用 Miller_Rabin，其基为 2,325,9375,28178,450775,9780504,1795265022，这样可以确保在long long的数据规模下准确判断（即若程序输出为1即为真素数，为0则为合数）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
inline ll qmul(ll x,ll y,ll mod){
    return (x*y-(ll)((long double)x/mod*y)*mod+mod)%mod;     
}

ll qpow(ll a,ll n,ll mod)/{
    ll res=1;
    while(n){
        if(n&1) res=qmul(res,a,mod);
        a=qmul(a,a,mod);
        n>>=1;
    }
    return res;
}

bool Miller_Rabin(ll n){
    if(n<3 || n&1==0) return n==2;
    ll u=n-1, t=0;
    while(u&1 == 0) u/=2, t++;
    ll ud[]={2,325,9375,28178,450775,9780504,1795265022};
    for(ll a:ud){
        ll v=qpow(a,u,n);
        if(v==1 || v==n-1 || v==0) continue;
        for(int j=1; j<=t; j++){
            v = qmul(v,v,n);
            if(v==n-1 && j!=t){ v=1; break; }
            if(v == 1) return 0;
        }
        if(v != 1) return 0;//Fermat检验
    }
    return 1;
}

inline ll rho(ll p){
    ll x, y, z, c, g, i, j;
    if(Miller_Rabin(p)) return p;
    while(1){
        y = x = rand()%p;
        c = rand()%p + 2;
        i = 0, j = 1, z = 1;
        while(i++){
            x = (qmul(x,x,p) + c) % p;
            z=qmul(z, abs(y-x), p);
            if(x==y || !z) break;
            if(i%127==0 || i&(i-1)==1){//分别在i=2^n 和 i%127==0时求gcd
                g = __gcd(z,p);
                if(g > 1) return g;
                if(i == j) y=x, j<<=1;
            }
        }
    }
}
0%