编译复习 (1)

发表于
主要关于编译原理引论部分和词法分析部分的复习整理。

引论

一些基概念

下面主要通过一些问题，来详细了解几个基础的概念，如翻译程序、编译程序、编译语言、高级语言。

  1. 什么是翻译程序、编译程序?

编译程序：把某一种高级语言程序等价地转换成另一种低级语言程序（如汇编语言或机器语言程序)的程序。(C/C++)

解释程序：把源语言写的源程序作为输入，但不产生目标程序，而是边解释边执行源程序本身。（Java/Python）

  1. 编译程序和解释程序的区别是什么?

编译程序和解释程序的主要区别是是否产生二进制文件，而在等价转化和优化处理方面基本是相同的。

  1. 编译程序的分类

诊断编译程序（用于程序开发和诊断） 优化编译程序（用于提高目标代码效率） 交叉编译程序（用于产生不同于宿主机的机器代码) 可变目标编译程序（如果不需要重写其中的与机器无关的部分就能改变目标机)

  1. 编译语言与和高级语言

高级语言相比编译语言程序易读易理解，容易维护，节省程序设计时间；但是程序效率低。

  1. 遍

所谓 遍，就是对源程序或源程序的中间表示从头到尾扫描一次。阶段和遍是不同的概念，一遍可以由若干段组成（词法分析，语法分析、中间代码程序可以合成一遍来处理），一个阶段可以分为若干遍来完成（比如：优化就可能分为好多遍）。

编译程序的生成

一般事实上有两种情况，一种是利用已有的某种语言的编译程序实现另一种语言的编译程序，另一种是把一种机器上的编译程序移植到另一种机器上（同一种语言）。

  • 利用已有的某种语言的编译程序实现另一种语言的编译程序。

如下图所示，假设我们有 格式机器指令的编译器 可以将 语言转化为 格式机器指令（对应下面的 T 形）。现在我们需要一个 格式机器指令的编译器可以将 语言转化为 格式机器指令的编译器（对应右边的 T 形）。

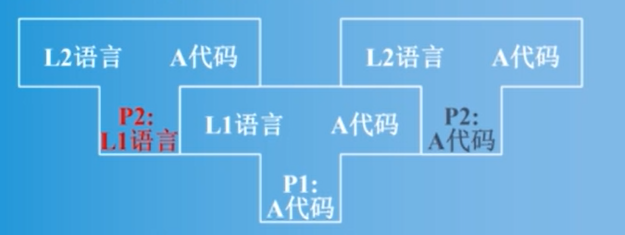
我们只需要实现一个 语言的编译器可以将 语言转化为 格式机器指令的编译器（对应左边的 T 形），此时注意编译器使用 编写的，无法被机器直接执行，我们使用编译器 ，将其编译为 格式机器指令即可。

  • 把一种机器上的编译程序移植到另一种机器上（同一种语言）。

如下图所示，假设我们有 格式机器指令的编译器 可以将 语言转化为 格式机器指令（对应最下面的 T 形）。现在我们需要一个 格式机器指令的编译器可以将 语言转化为 格式机器指令的编译器（对应最右边的 T 形）。

  1. 实现一个 语言的编译器可以将 语言转化为 格式机器指令的编译器 ，
  2. 编译 ，得到 格式机器指令的编译器 可以将 语言转化为 格式机器指令。
  3. 编译 ，得到 格式机器指令的编译器 可以将 语言转化为 格式机器指令。

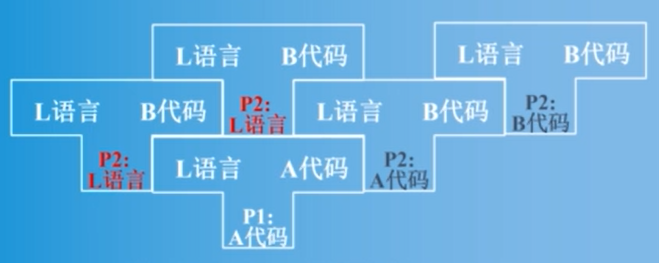
编译程序的基本原理

假设一个精通中文和日文的英国人，要将中文翻译为日文。那么他首先会将中文翻译成自己熟悉的英文，再将英文转化为日文。具体而言，编译程序也是类似，主要包含五个阶段，词法分析、语法分析、语义分析和中间代码生成、优化、目标代码生成，对照上面的例子，其具体流程如下：

  • 识别出句子中的一个个单词；词法分析
  • 分析句子的语法结构；语法分析
  • 根据句子的含义进行初步翻译；语义分析与中间代码产生
  • 对译文进行修饰；优化
  • 写出最后的译文；目标代码产生

对于每个部分，我们简要介绍其任务、原则和描述工具以及一些其他性质，关于这些内容的详细过程在后面的章节中会详细讲述。

  1. 词法分析

任务：输入源程序，对构成源程序的字符串进行扫描和分解，识别出一个个单词符号。

依循的原则：词法规则（构词规则）

描述工具：正规式和有穷自动机

  1. 语法分析

任务：在词法分析的基础上，根据语言的语法规则把单词符号串分解成各类语法单位。

依循的原则：语法规则

描述工具：上下文无关文法

  1. 语义分析和中间代码产生

任务：对各类不同语法范畴按语言的语义进行初步翻译。

依循的原则：语义规则

描述工具：属性文法

中间代码：三元式，四元式，树形结构等

  1. 优化

任务：对于前阶段产生的中间代码进行加工变换，以期在最后阶段产生更高效的目标代码。

依循的原则：程序的等价变换规则

  1. 目标代码生成

任务：把中间代码变换成特定机器上的目标代码。

依赖于：硬件系统结构和机器指令的含义

目标代码三种形式：绝对指令代码，可直接运行；可重新定位指令代码，连接装配；汇编指令代码，需要进行汇编。

编译前端与后端

编泽前端：与源语言有关但与目标机无关的那部分，如词法分析，语法分析，语义分析与中间代码产生，与机器无关的优化

编译后端：与目标机有关那部分，如与目标机有关的优化，目标代码产生

词法分析

词法分析器

词法分析的现实任务

词法分析是指从左至右逐个字符地对源程序进行扫描，产生一个个单词符号。在编译中主要作用是把作为字符串的源程序改造成为单词符号串的中间程序，以便于后续的语义分析等等。在编译器中，一般而言词法分析的功能都是由 词法分析器 承担的，简而言之其就是一段执行词法分析的程序。

现在我们关注这一部分的输入和输出。作为最早的一个阶段，其输入是很显然的——要翻译的源程序，其输出应当是一些单词符号，具体我们会对这些符号按照类型进行划分，就像语文中我们会将句子中的词语划分为 主语、谓语、宾语 等等，这对我们后续分析是有帮助的。

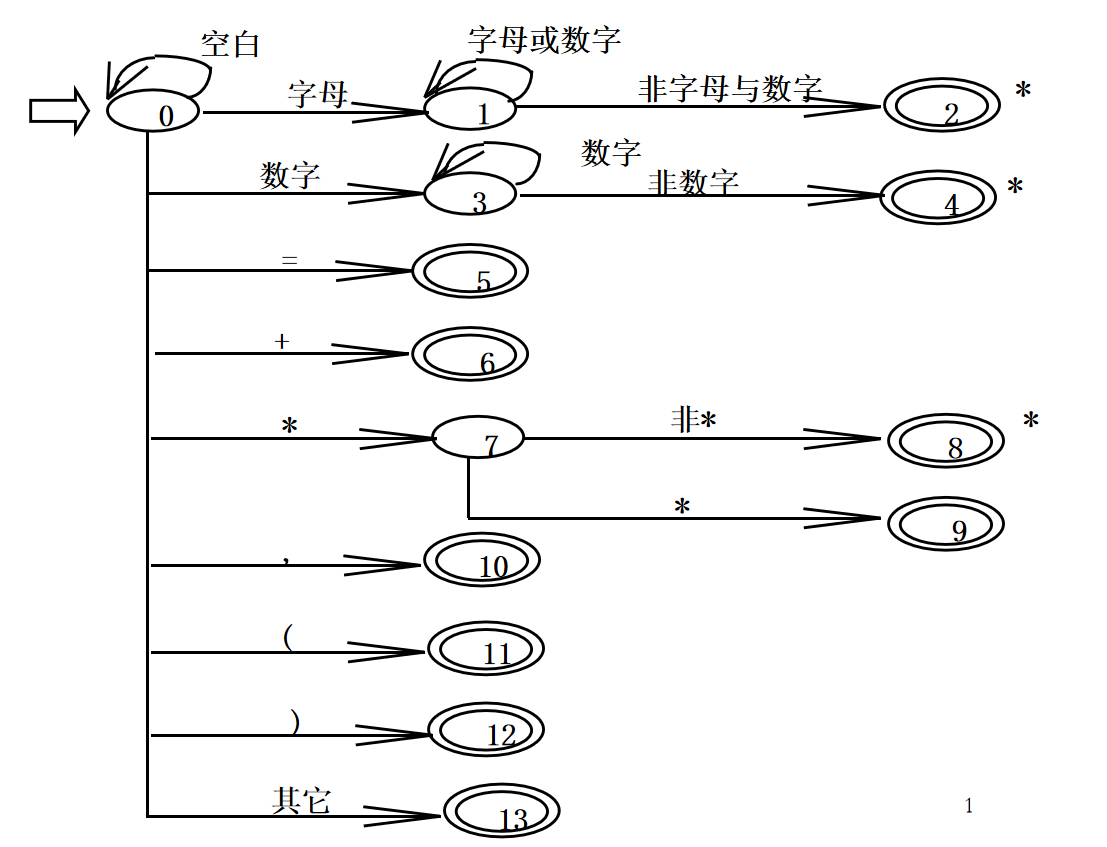
单词类型可以分为如下部分：

  • 基本字：如 begin，repeat

  • 标识符，表示各种名字：如变量名、数组名和过程名

  • 常数：各种类型的常数

  • 运算符：

  • 界符：逗号、分号、括号和空白

具体而言，输出的单词符号的表示形式为 单词种别，单词符号的属性值，这有点像一个字典，对应着键名和键值。单词种别通常用整数编码表示。若一个种别只有一个单词符号，则种别编码就代表该单词符号。一般来说，基本字、运算符和界符都是符一种。若一个种别有多个单词符号，则对于每个单词符号，给出种别编码和属性信息。标识符单列一种；标识符的属性就是存放它的有关信息的符号表项的指针。常数按类型分种；常数的值则表示成标准的二进制形式。

我们举两个例子讲述上面过程：

  1. C程序 while(i >= j) i--;；我们输出的符号为
1
2
3
4
5
6
7
8
(while, )
("(", )
(id,指向的符号表项的指针)
(">=", )
(id,指向的符号表项的指针)
(")", )
(id,指向的符号表项的指针)
(--, )
  1. FORTRAN程序 IF (5.EQ.M) GOTO 100；我们输出的符号为
1
2
3
4
5
6
7
8
逻辑IF (34,-)
左括号 (2,-)
整常数 (20,101) #这里101表示5的二进制形式
等号 (6,)
标识符 (26,M)
右括号 (16,-)
GOTO (30,-)
标号 (19,100)

这里老师上课留了一个问题 为何将词法分析作为一个独立的阶段？是否应当将其处理为一遍呢？ 一个观点是：作为独立阶段的优点，可以 简化编译器的设计，降低语法分析的复杂性；提高编译效率；增加可移植性。不作为一遍，将其处理为一个子程序，是因为词法分析可以与语法分析在一遍中完成，故我们可以将其合并，每当语法分析器需要一个单词符号时就调用这个子程序。

具体而言，词法分析器和语法分析器操作关系如下图所示

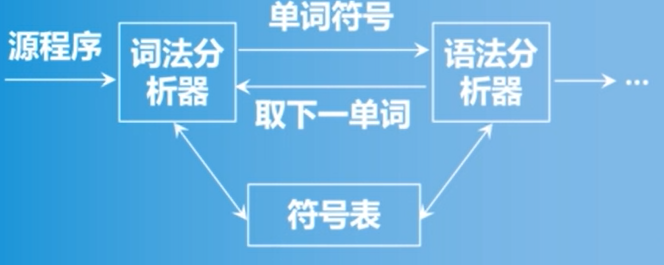
词法分析器的设计

上面我们已经知道了具体词法分析器的任务作用，故可以设计其大致流程如下

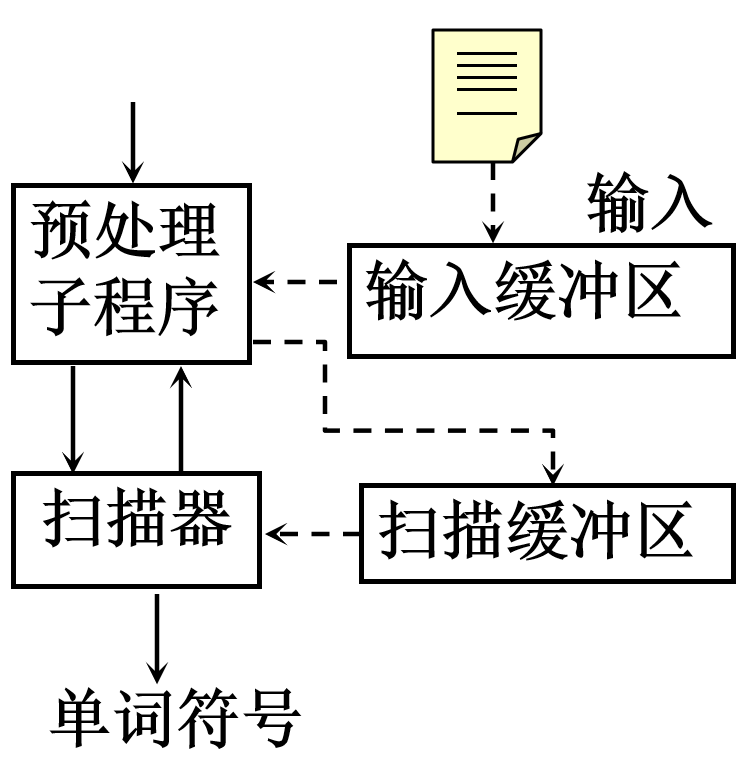
具体每个过程我们做下面阐述：

  • 预处理子程序：剔除无用的空白、跳格、回车和换行等编辑性字符;区分标号区、捻接续行等

  • 扫描缓冲区：起点指示器指向当前正在识别的单词符号的开始位置；搜索指示器用于向前搜索以寻找单词的终点。

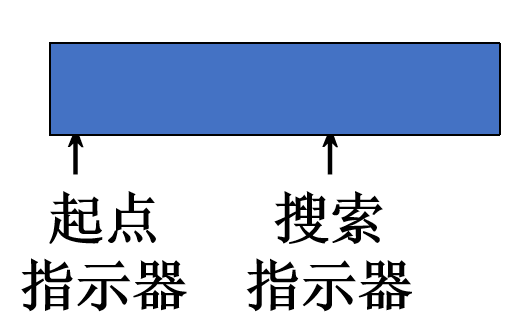
字母表

在我们进行实际的词法分析之前，首先需要介绍一些数学概念，这里由于其内容篇幅较长，对于每个重要的数学知识部分，我们单立一小节。

定义（字母表、字母和字）。字母表是一个非空有穷集合记作 。字母表 $中的元素称为该字母表的一个字母，也叫做字母表上的字符（或符号）。字母表中符号组成的有穷序列称为上的字符串，也称为$上的字或者句子，不包含任何字符的序列称为空字，记作 。事实上对于一种高级程序设计语言而言，它的字母表就是该语言的有效字符集。

一些用于帮助理解的例子是

就是一个字母表， 是该字母表上的字； 表示 上的所有字组成的集合。

下面我们定义一些在 上的运算。

  • 的子集 和 的连接（积）定义为 （就是笛卡尔积）
  • 自身的 次积记为
  • 规定 ，令 是 的闭包（克林闭包）
  • 记 ，称 是 的正则闭包。

对于上面运算规则，我们同样给出例子

例设 是一个字母表，则

＝ 是否成立？

不成立。如果 包含 ，则 ，故

定义（语言和句子） 设 $$ 是一个字母表， 的任意子集 称为字母表 上的一个语言。对于 叫做 的一个句子。

正规式和正规集

正规集，也称为正则集，它是由一条正则式定义出来的语言。正则式 由正则运算符和正则操作符组合而成，它可以匹配一系列的字符串。正规集的定义方式有很多种，包括有限自动机、正则文法、扩充文法等等。

对给定的字母表

  1. 和 都是 上的正规式，它们所表示的正规集为 和

  2. 任何 ， 是 上的正规式，它所表示的正规集为

  3. 假定 和 都是 上的正规式，它们所表示的正规集为 和 ，则

  • 为正规式，它所表示的正规集为

  • 为正规式，它所表示的正规集为

  • 为正规式，它所表示的正规集为

  • 可以看出 为一个积性函数

仅由 有限次 使用上述三步骤而定义的表达式才是 上的正规式，仅由这些正规式表示的字集才是 上的正规集。注：正规式的运算符 | 读为或， 读为 连接，* 读为闭包（任意有限次的自重复连接)

若两个正规式所表示的正规集相同，则称这两个正规式 等价。如b(ab)* = (ba)*b = (a*b*)* = (ab)*

对于正规式我们给出一些相关的数学性质：

交换律： 结合律： 结合律： 分配律： 分配律：

一些帮助理解的例子：

设 是一个字母表，则 是正规式； 是正规式； 是正规式；

C语言标识符的正规式为 (letter|_)(letter_|digit)*，其所表示的正规集即为所有以字母或下划线开头的字母、数字和下划线组成串的集合。

产生 形式的正规式是？ 答案： 或者

正规文法

定义

文法是用来描述语言语法结构的形式规则，正规文法是用来描述词法结构的形式规则。正规文法 定义为四元组 ，其中

  • ：终结符集合（非空有限集）
  • ：非终结符集合（非空有限集），且
  • ：文法的开始符号，
  • ：产生式集合（有限），每个产生式形式为 或 ，
  • 开始符 至少必须在某个产生式的左部出现一次。

几点规定

  • 可以缩写为 ，其中，| 读成 或，每个 称为 的一个候选式
  • 表示一个文法时，通常只给出开始符号和产生式。例：
  • 如果 ，则我们称这个序列是从 到 的一个 推导。若存在一个从 到 的 推导，则称 可以推导出 。
  • 文法的语言 指文法产生（开始符号出发推导）的所有终结符串构成的集合，

文法 的语言是

文法 的语言是

注意符号 和 的不同用法。

一般上 表示直接推导，也就是直接存在的产生式； 表示推导，就是经过若干个

若产生式形如 或 ，则称 为右线性文法，两者等价。这里的线性是因为对于上述文法的推导始终具有线性结构。

如文法

转换成右线性文法，将 转换为

一些栗子：

所有含子串 011 的由 0 和 1 构成的符号串的全体。

以 a 开头和结尾的所有小写字母串（包含单个a)。

C语言的标识符集是由以字母或下划线开头的字母、数字和下划线组成的串的集合，生成该集合的正规文法为，下面 digit 和 letter 分别表示所有数字和字母

无符号整数的正规文法为 若最高位不可为0

为表示方便，对正规式进行命名，并用名字来引用相应的正规式

定义（正规定义式）令 是基本符号的字母表，那么正规定义式是如下形式的序列 。其中，各个 的名字都不同，每个 都是 上的正规式。

一些栗子：

C语言标识符集合的正规定义式

正规文法和正规式的等价性

正规文法和正规式等价，即对任意一个正规文法，存在一个定义同一语言的正规式，反之亦然。

正规文法转换为等价的正规式

给定一个正规文法 ，，，，利用以下转换规则对文法的产生式进行转换：

  • 若 ,并且 ，则将两个产生式转化为 。

  • 若 ,并且 ，则将两个产生式转化为 。

  • 若 ,并且 ，则将两个产生式转化为 。

不断应用规则 ①~ ③，直至只剩下一个开始符号定义的正规定义式，并且正规定义式的右部不含非终结符，此时所得到的正规定义式的右部即为所求的等价正规式。

两个栗子：

设有正规文法

该文法生成语言的正规式：

首先将最后一个产生式带入倒数第二个有：，即

故

将正规文法 ,换成正规式.

由 有 ，同理有

故原来的文法可以转换为

正规式文法转换为等价的正规文法

将 上的正规式 转化为正规文法

  • 令 ，对任何正规式 ，选择一个非终结符，如 ，生成 → ，并将 作为文法的开始符号。

2.按照如下规则对 以及分解过程中所产生的各个正规定义式进行分解。

  • 若 是正规式，对形如 的产生式，重写为 ，其中 为新的非终结符。

  • 若 是正规式，对于对形如 重写为 。

  • 若 是正规式，对于对形如 重写为 。

一个栗子：

将正规式为 ，转换为正规文法

首先分解为 ，两个产生式形式是一样的，我们仅解释其中一个。

第一个产生式可以进一步转化为

然后是

最后有

故最终结果为

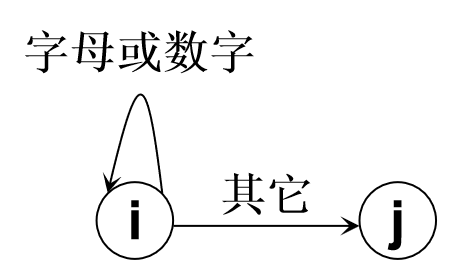
状态转换图

状态转换图是一张有限方向图。用来进行词法分析器的构造。

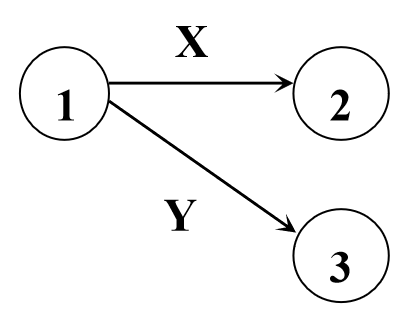
  • 结点代表状态，用圆圈表示。

  • 状态之间用箭弧连结，箭弧上的标记(字符)代表射出结点状态下可能出现的输入字符或字符类。

  • 一张转换图只包含有限个状态，其中有一个为初态，至少要有一个终态（用双圈表示）。

  • 从初态出发到所有终态的路径上连接的字符串是状态转换图识别的单词集合。

  • 它是设计词法分析程序的一种好途径.

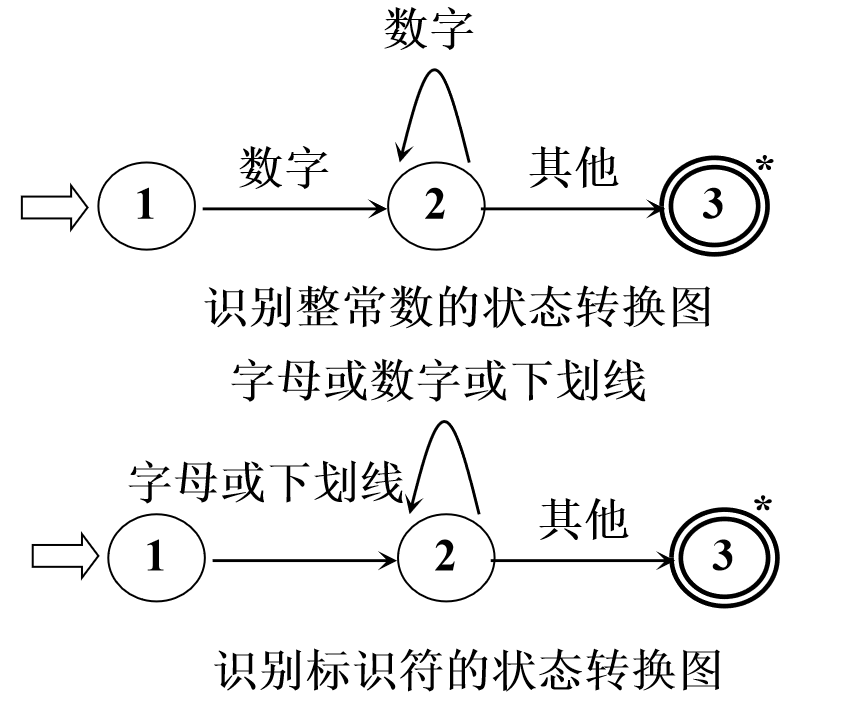
如何容易的设计出识别 、 的状态转换图？

一个状态转换图可用于识别（或接受）一定的字符串

有穷自动机

利用状态转换图识别单词

对于识别过程，我们做出如下限制：

  • 所有基本字都是保留字；用户不能用它们作自己的标识符
  • 基本字作为特殊的标识符来处理不用特殊的状态图来识别，只要查保留字表。
  • 如果基本字、标识符和常数(或标号)之间没有确定的运算符或界符作间隔，则必须使用一个空白符作间隔。例如 ifj>0 要写成 if j>0

同样值得说明的是，上面的限制实际上是不严格的，对于一般给定的程序语言，几乎都满足上述条件。

那么根据基本的识别要求，我们可以使用如下状态转换图识别单词

接下来我们考虑实现上面的状态转化图，一个主要的思想是将上述每个状态对应为一小段程序进行处理。另外我们需要先给出一些可能用到的全局变量和过程(函数)

  • ch 字符变量、存放最新读入的源程序字符
  • strToken 字符数组，存放构成单词符号的字符串
  • GetChar 子程序过程，把下一个字符读入到 ch 中
  • GetBC 子程序过程，跳过空白符，直至 ch 中读入一非空白符
  • Concat 子程序，把ch中的字符连接到 `strToken``
  • `IsLetter 和 IsDisgital 布尔函数，判断ch中字符是否为字母和数字
  • Reserve 整型函数，对于 strToken 中的字符串查找保留字表，若它是保留字则给出它的编码，否则回送0
  • Retract 子程序，把搜索指针回调一个字符位置
  • InsertId 整型函数，将strToken中的标识符插入符号表，返回符号表指针
  • InsertConst 整型函数过程，将strToken中的常数插入常数表，返回常数表指针。一、状态转换图的实现

下面我们详细讨论处理的一些细节

  1. 对不含回路的分叉结，可用一个CASE语句或一组IF-THEN-ELSE语句实现

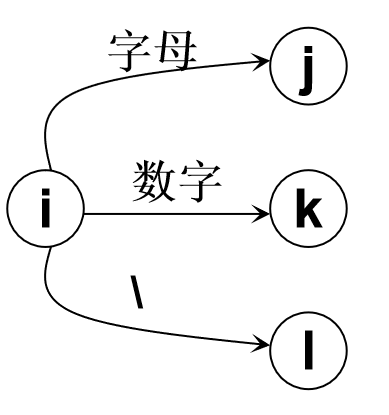
1
2
3
4
5
GetChar( );
if IsLetter( ) {…状态j的对应程序段…;}
else if IsDigit( ) {…状态k的对应程序段…;}
else if (ch=‘\’) {…状态l的对应程序段…;}
else {…错误处理…;}

  1. 对含回路的状态结，可对应一段由WHILE结构和IF语句构成的程序.

1
2
3
4
GetChar();
while IsLetter( ) or IsDigit( )
   GetChar();
状态j的对应程序段
  1. 终态结表示识别出某种单词符号，因此，对应语句为 RETURN (C，VAL) 其中，C 为单词种别，VAL 为单词自身值.
有穷自动机(DFA)

为了讨论词法分析的自动生成，需要将上述状态图的概念形式化。故我们引入 有穷自动机（Determine Finite Automaton）。

其定义如下：

确定有穷自动机 是一个五元式 ，其中：

  1. ：有穷状态集，
  2. ：输入字母表(有穷)，
  3. ：状态转换函数，为 的 单值 部分映射， 表示：当现行状态为 ，输入字符为 时，将状态转换到下一状态 。我们把 称为 的一个后继状态。
  4. 是唯一的一个初态；
  5. ：终态集(可空)。

具体而言上面五个元素还是很好理解的：作为一个自动机，首先我们确定所有可能地状态集 、字符集 ，并且确定初始状态 ；接下来我们需要初态开始，不断进行状态的变化 最终达到终态 。值得注意的是有穷自动机的状态转移函数必须为单射，简单来说就是对于每个当前状态和接下来输入的字符，经过状态转化有唯一确定的结果。这也就是为什么其称为 有穷自动机 。当然如果其不是单射，比如对于状态 ，接收字符 ，有 ，那么我们将不能确定到底接下来的状态是 2 还是 3。

对于 中的任何字 ，若存在一条从初态到某一终态的道路，且这条路上所有弧上的标记符连接成的字等于 ，则称 为 DFA 所识别(接收)。若 的初态结点同时又是终态结点，则空字 可为 所识别（接收）。DFA 所识别的字的全体记为 。

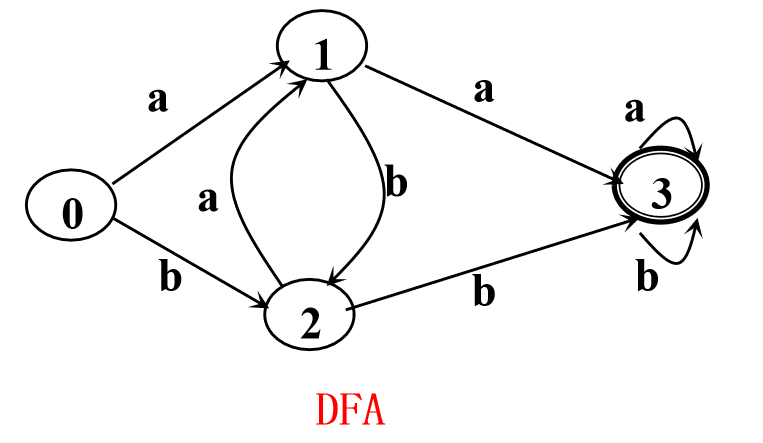
一个栗子：

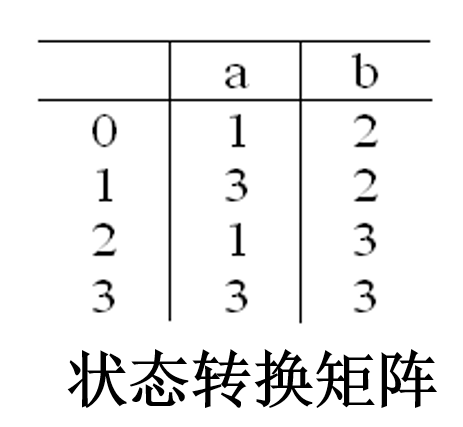
DFA ，其中 定义如下：

1
2
3
4
>f(0，a)=1		f(0，b)=2
>f(1，a)=3 	 	f(1，b)=2
>f(2，a)=1		f(2，b)=3
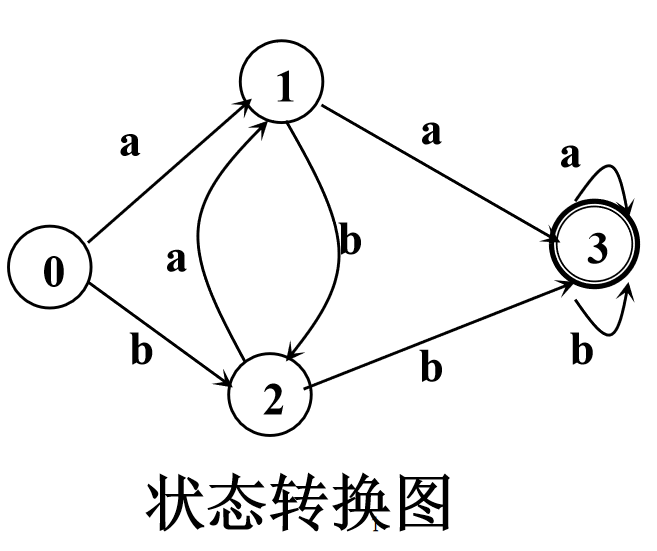
>f(3，a)=3 		f(3，b)=3

那么可以得到状态转化矩阵

状态转化图

可以看到，DFA 能被表示为状态转换图。假定DFA M含有 个状态和 个输入字符，那么，这个图含有 个状态结点；每个结点顶多含有 条箭弧射出；且每条箭弧用 上的不同的输入字符来作标记。

非确定有限自动机(NFA)

与确定有限自动机相对，同时我们还有非确定有限自动机(NFA)。一个非确定有限自动机(NFA) M是一个五元式 ，其中：

  1. ：有穷状态集，
  2. ：输入字母表(有穷)，
  3. ：状态转换函数，为 的 部分映射
  4. 是唯一的一个初态；
  5. ：终态集(可空)。

可以得到两者之间的区别（两者只有第三条存在差异）：

  • 弧上的标记可以是 中的一个字，而不一定是单个字符；也可以是空字。
  • 同一个字可能出现在同状态射出的多条弧上。由于 ，可以看出 是的特例。

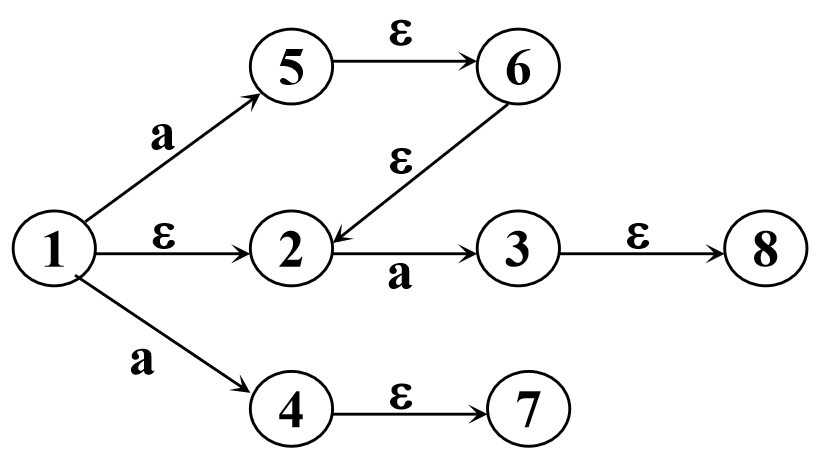
一个NFA的状态转化图

两者的性质

对于任何两个有限自动机 和 ，如果 ，则称 与 等价。

自动机理论中一个重要的结论：判定两个自动机等价性的算法是存在的。

对于每个存在一个，使得。亦即与描述能力相同。

可以看到，NFA设计词法分析器更方便（因为状态转移输入的字符不必要是一个字符）；但同时我们必须使用 DFA用来自动生成最后的程序（程序的必须具有确定性）

NFA到DFA的转化

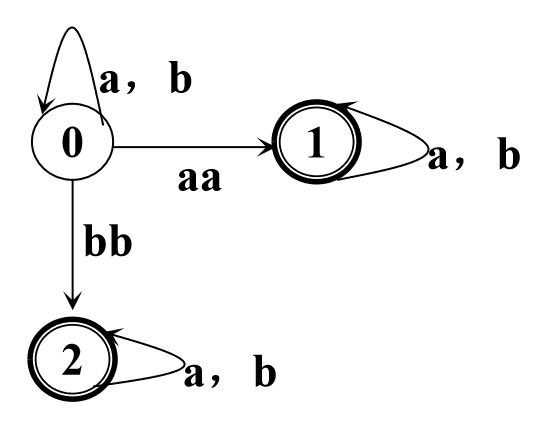
先看一个例子，我们有如下 NFA M

假设我们把状态 看作一个整体，那么有

此时可以看到我们完全将 NFA 转化到 DFA。下面我们给出相关的理论推导。

为了方便处理 NFA 中的空边，首先我们给出一个定义：

设 是 的状态集的一个子集，定义 的 为:

  1. 若 ，则 ；
  2. 若 ，则从 出发经过任意条 弧而能到达的任何状态 都属于

即 从某个出发经过任意条弧能到达 设 是 中的一个字符，定义 其中， 为 中的某个状态出发经过一条 弧而到达的状态集合。

一个栗子：

给定下面状态转化图

我们有

  • 设
  • 设 ，，，则 ，，，，，，

下面我们给出NFA到DFA的转化的详细算法

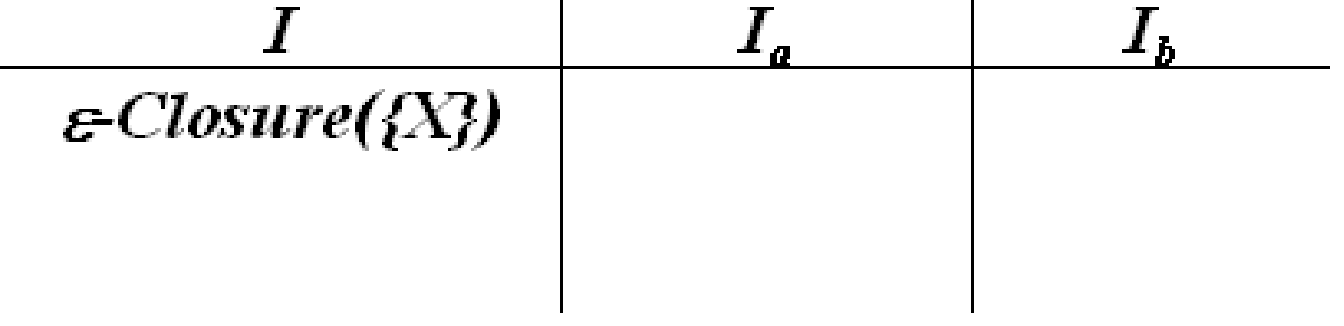
主要思想是通过上面基础定义，不断构建一个形如上图的状态转化矩阵。

  • 首先，置第 1 行第 1 列为 求出这一列的
  • 然后，检查这两个 ，看它们是否已在表中的第一列中出现，把未曾出现的填入后面的空行的第 1 列上，求出每行第2，3列上的集合
  • 重复上述过程，直到所有第2，3列子集全部出现在第一列为止。
习题

问题1：有穷自动机终态只能有一个。

解析：有穷自动机的终态可以有多个，故上面语句错误。

问题2：DFA 的边上可以显式地出现空字。

解析：NFA 的边上可以显式地出现空字。

问题3：NFA比DFA的能力稍强。

解析：事实上 NFA 和 DFA 两者之间是可以进行等价转化的，故两者能力应当相同。

问题4：自动机等价变换的基本思想是？

A.重新设计 B.变换状态 C.变换边 D.将状态集映射为单个状态

解析：D

问题5：状态集空字闭包函数的构成包括？

A.状态集自身的状态 B.初态 C.终态 D.状态集的状态通过连续空边达到的新状态

解析：A、D。

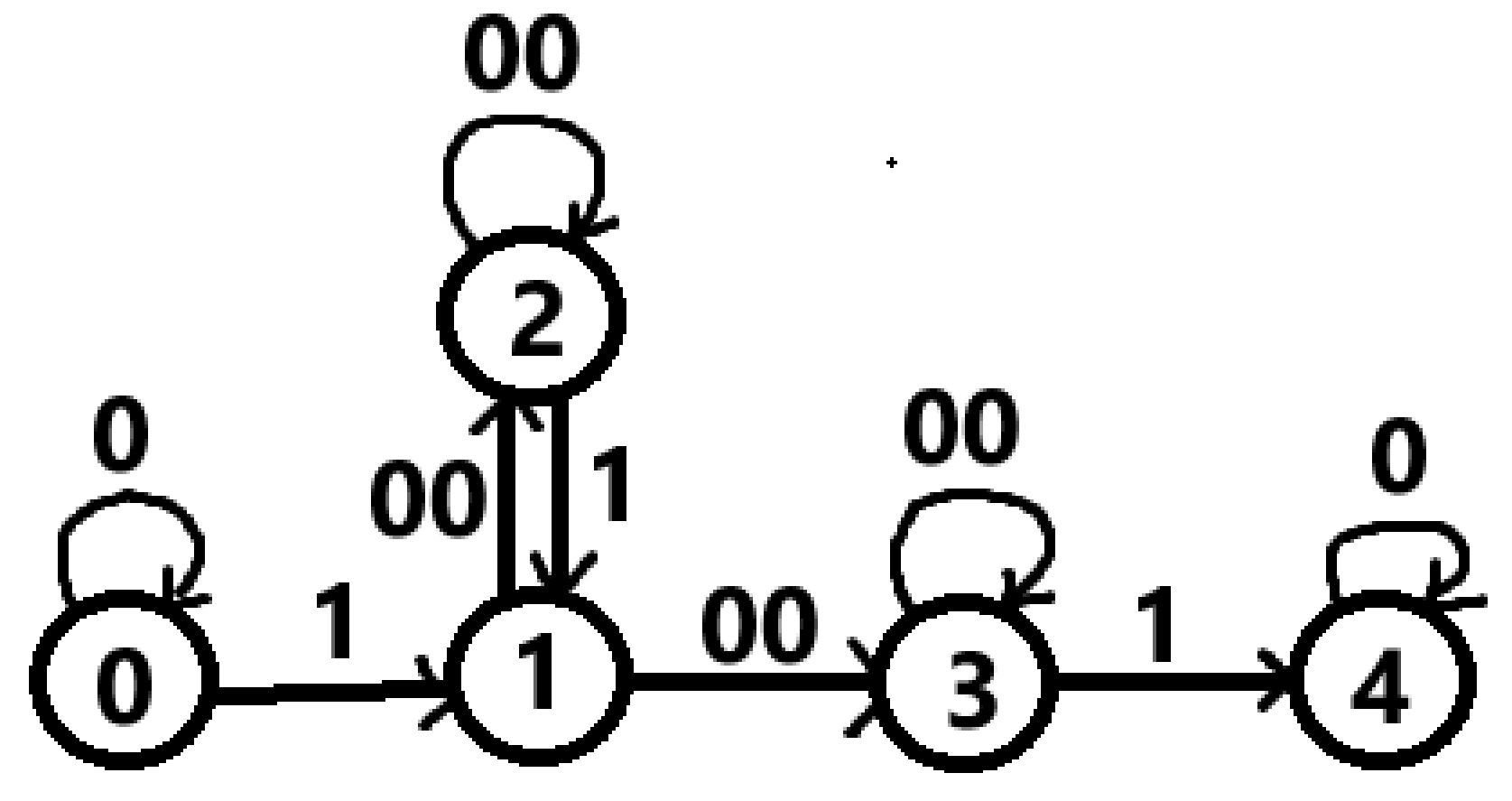
问题6：已知有语言 ，并且 中至少有两个 1，又在任何两个 1 之间有偶数个0， 试构造接受该语言的有穷自动机。(NFA即可，该题中偶数指大于等于2的数)

解析：

我们首先写出其正规式 故可以将其转化为如下状态转化图

DFA 的化简

基本原理

根据上面方法，我们已经可以方便地得到一个 DFA，但其形式有可能较为复杂，下面我们讨论如何对其进行化简，

为了后文便于描述，这里我们给出一些定义：

  • 对DFA M的化简：寻找一个状态数比 M 少的DFA M’，使得 。对用自动机原理设计的硬件，直接意味着节省成本，对软件则直接对应精炼高效的程序
  • 假设 和 为 的两个状态，称 和 等价。如果从状态 出发能读出某个字 而停止于终态，同样从 出发也能读出 而停止于终态；反之亦然，则两个 状态等价，否则则称它们是 可区别的。

我们化简的主要思想是 按照等价关系对状态集进行划分，每个子集中的元素进行合并。

具体而言，两个 状态等价 需要满足下面条件：

  • 假定状态 和 经 弧分别到达 和 ，而 和 属于现行 中的两个不同子集( 和不等价 )，说明有一个字 ， 读出 后到达终态，而 读出 后不能到达终态，或者反之。那么对于字 ， 读出 后到达终态，而 读出 不能到达终态，或者反之。所以 和 不等价。

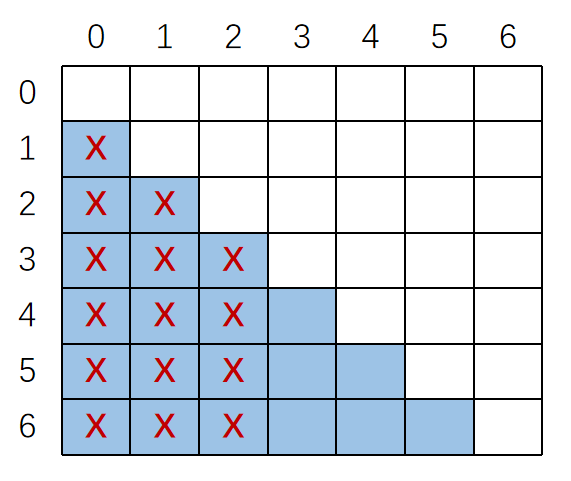
故下面可以给出具体的划分算法：

  • 为所有状态对 画一张表，开始时表中每个格子内均为空白（未做任何标记）
  • 对 的一切状态对 ，在相应的格子内做标记（ 终态和非终态一定是不等价的 ）。
  • 重复下述过程，直到表中内容不再改变为止：如果存在一个未被标记的状态对 ，且对于某个 已做了标记，则在 相应的格子内做标记。
  • 在完成1，2，3之后，所有未被标记的状态对 都是等价的，即 。

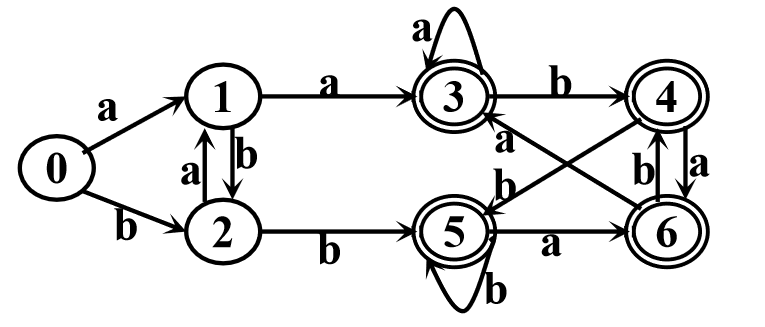
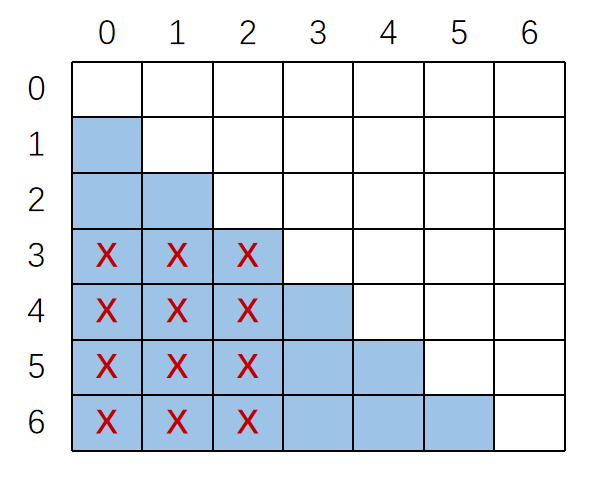
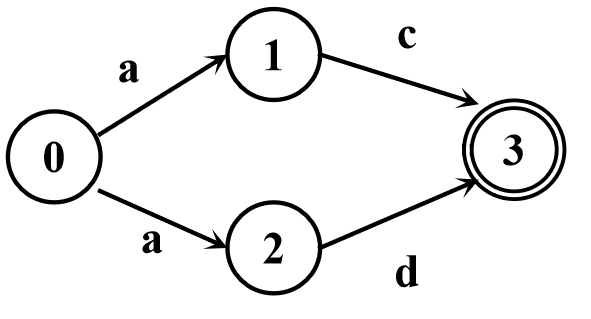
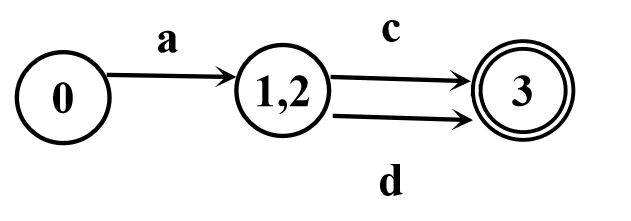
一个例子

标记终态和非终态有

对于 接收 分别转化为状态 ，而这两个状态是不等价的，故标记关系对 。 也是同理。此时有

对于关系对 则不发生改变，故最终可以将 合并为一个状态，并有结果如下

习题

问题1：状态 和 接收字母表 中 后到达同样的状态，接收 后 达到终态，达到空集。 和 也是等价的。

解析： 错误

问题2：自动机化简的思想是划分等价状态集合，然后每个集合留一个状态。

解析： 正确

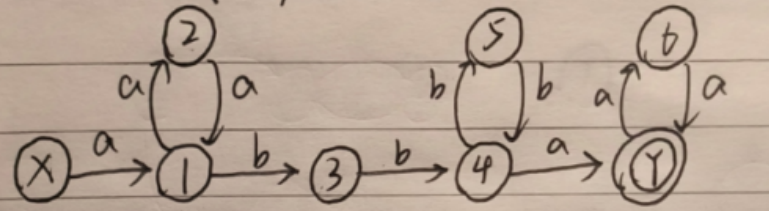
问题3：设有 (1)给出描述该语言的正规式。 (2)构造识别该语言的最小化的确定有穷自动机。

解析：

  1. 其正规式为

  2. 首先构造 NFA 如下

首先标记终态与非终态

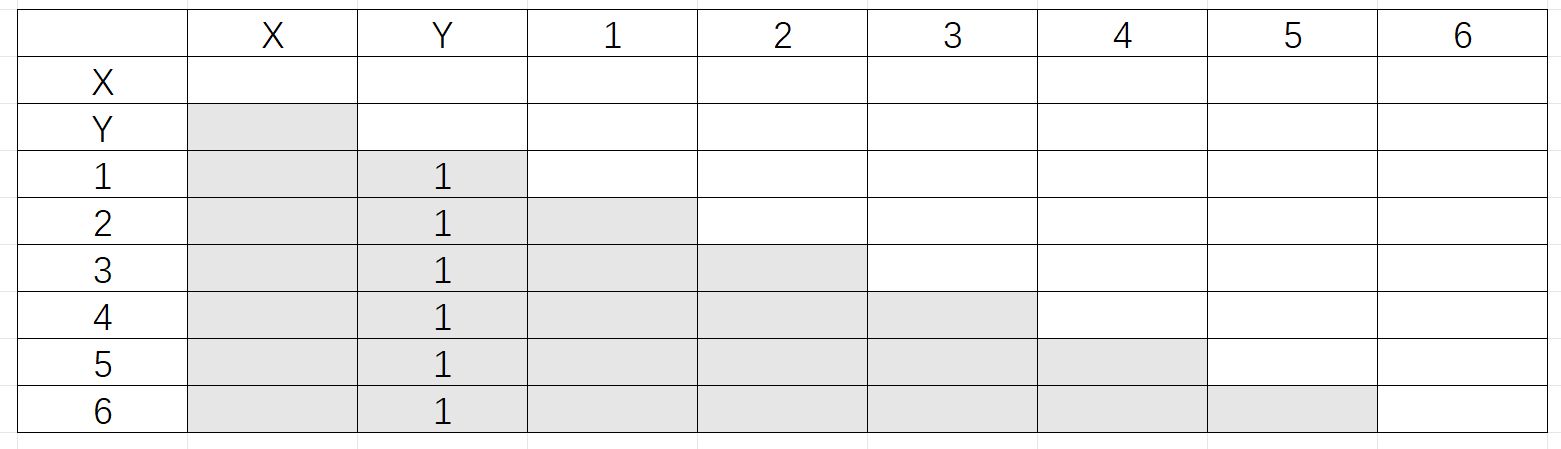
其次根据状态能接收字符集的不同继续标记。 接收 ； 接收 ； 接收 ；

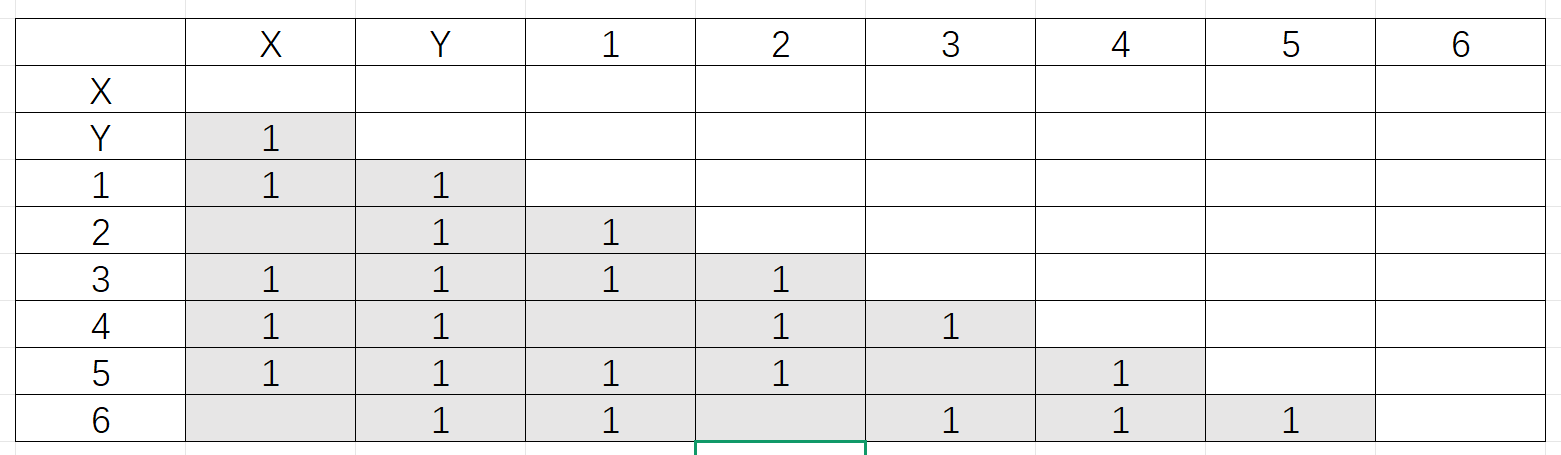
最后根据状态转移

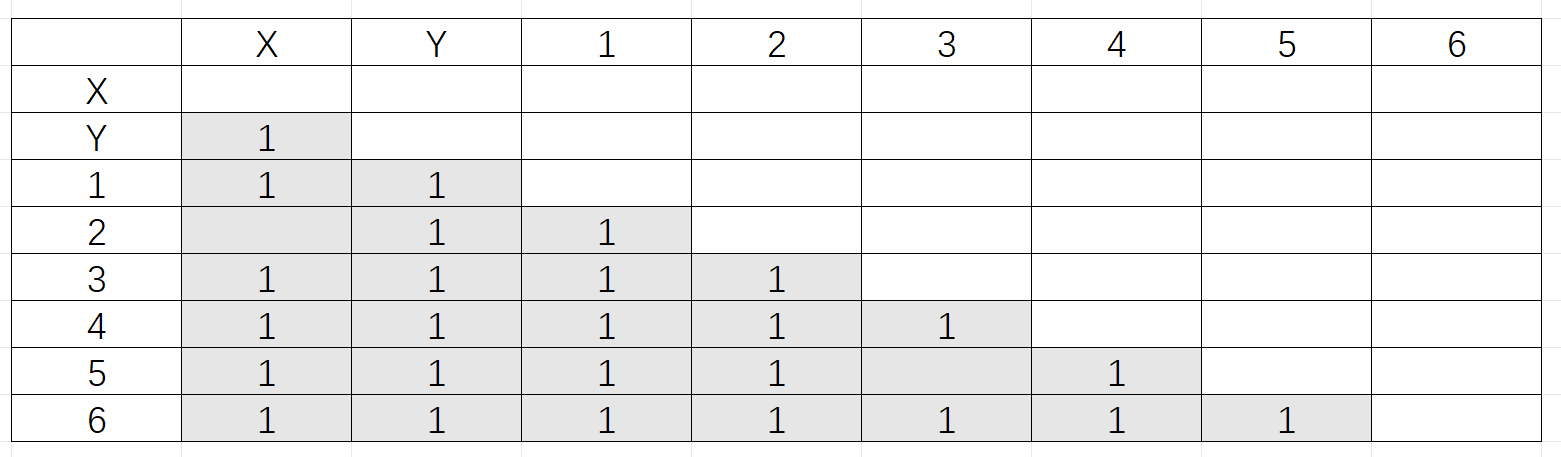
故合并后有

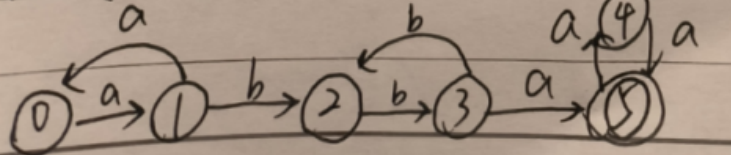
问题4：设 为一非确定的有穷自动机，其 定义如下 ，试构造与之等价的确定的有穷自动机D,并对所构造的自动机进行最小化。

总结

总的来说，需要掌握下图中的所有的等价转化。

0%